Etude scientifique publiée le 24 Mai 2018.
Sommaire
L’introduction de gènes extérieurs (outcross) devrait réduire le taux de consanguinité et les effets négatifs associés dans les populations fortement consanguines. Dans cette étude, nous avons examiné l’efficacité de différents schémas d’outcrossing en utilisant des simulations informatiques. Le taux de consanguinité estimé sur une période de 25 ans de 2,1 % par génération dans une race de chien fortement consanguine a été réduit à 1,8 % lorsqu’une seule portée était produite par un outcross sans retours croisés. Pour réduire le taux de consanguinité en dessous de 1 %, plus de huit des 14 portées annuelles de la race réceptrice devaient être issues d’un outcross. Cependant, dans les races de chiens de pedigree, l’outcrossing est généralement suivi de retours croisés et implique souvent une ou quelques portées. Les retours croisés réduisent considérablement l’effet de l’outcrossing. Lorsque deux portées étaient produites par un outcross suivi d’une génération de retour croisé, le taux de consanguinité était de 2,0 % par génération. Un outcrossing continu s’avérait plus efficace qu’un seul ou quelques outcross. Lorsqu’une probabilité de 5 % était donnée à chaque portée née au cours de 25 ans d’être produite par un outcross, le taux de consanguinité a été réduit à -0,2 %. Pour examiner la possibilité d’introduction de nouveaux allèles de la population donneuse à la population réceptrice, le destin de différents types d’allèles (allant de complètement létaux à bénéfiques) avant et après un outcross a été étudié en simulant d’abord 80 ans de sélection naturelle avant l’outcross, puis différents types d’outcross. La sélection naturelle ayant réduit la fréquence des allèles létaux avant l’outcrossing, l’introduction d’un allèle létal, qui était présent dans la race donneuse mais pas dans la race réceptrice, s’est produite rarement. L’introduction d’allèles légèrement néfastes ou neutres s’est produite plus fréquemment. En conclusion, l’outcrossing n’a eu qu’un effet limité à court terme, sauf s’il était répété de manière continue. Néanmoins, il pourrait aider à gagner du temps pour changer la structure de la population afin d’augmenter la taille efficace de la population.
1 INTRODUCTION
Dans les populations fortement consanguines, la diversité génétique peut être si faible et les troubles génétiques si courants que la seule possibilité de survie de la race est l’outcrossing avec des individus d’autres populations. Dans les races de chiens de pedigree, l’outcrossing a été proposé pour restaurer la diversité génétique et surmonter une forte prévalence de troubles génétiques, par exemple, chez le Lundehund norvégien (Stronen et al., 2017) et le Griffon Bruxellois (Knowler, Berg, McFadyen, La Ragione, & Rusbridge, 2016). Dans les populations sauvages, il existe plusieurs exemples où un seul individu a restauré la diversité génétique, par exemple, chez le loup (Johnson et al., 2010), chez la panthère de Floride (Vila et al., 2003) et chez le hamster commun (La Haye, Koelewijn, Siepel, Verwimp, & Windig, 2012). Ce succès de l’outcrossing est appelé « sauvetage génétique ». Cependant, le sauvetage génétique dans les populations sauvages ne semble pas toujours fonctionner (Tallmon, Luikart, & Waples, 2004). Par exemple, chez le loup gris, après des effets initiaux positifs d’un seul individu entrant dans une population fortement consanguine, la population est de nouveau au bord de l’extinction (Hedrick, Peterson, Vucetich, Adams, & Vucetich, 2014). Selon Whiteley, Fitzpatrick, Funk, & Tallmon, (2015), « Le sauvetage génétique peut ne pas sauver les populations en péril à long terme… mais peut gagner du temps en améliorant la condition physique et en augmentant les tailles de population à court terme. » Chez les chiens, les recherches manquent pour déterminer quand l’outcrossing peut réussir ou non.
L’outcrossing peut fonctionner parce que les individus de races différentes sont moins ou même non apparentés, par rapport aux individus au sein de la race. Les descendants consanguins sont produits par l’accouplement d’individus apparentés, et plus les parents sont apparentés, plus le coefficient de consanguinité des descendants est élevé. Les individus non apparentés produisent toujours des descendants avec un coefficient de consanguinité (F) de 0, quel que soit leur propre niveau de consanguinité. Par conséquent, lorsque des individus de races différentes sont accouplés, leurs descendants seront moins ou même pas du tout consanguins. La dépression consanguine est principalement causée par des allèles délétères récessifs (Lynch & Walsh, 1998; Roff, 1997). Ces allèles peuvent atteindre des fréquences relativement élevées par dérive génétique dans les populations avec une petite taille effective. Cependant, en raison de la nature aléatoire de la dérive génétique, en général, différents allèles dérivent vers des fréquences élevées dans différentes populations, sauf dans de rares cas où il y a eu (indirectement) sélection dans les deux races pour le même allèle délétère, par exemple lorsqu’il y a un allèle étroitement lié sous sélection. Ainsi, avec un outcross, la fréquence d’un allèle délétère spécifique avec une fréquence élevée est, au moins théoriquement, censée être réduite.
Le revers de l’outcrossing est que la race réceptrice peut perdre sa spécificité. La moitié du génome des descendants d’un outcross provient de la race donneuse et, par conséquent, ils peuvent s’écarter considérablement du standard de la race. Pour éviter de trop changer les caractéristiques de la race, une race apparentée est utilisée comme race donneuse et les descendants résultants sont soigneusement examinés et sélectionnés selon le standard de la race, puis croisés avec des animaux de la race réceptrice. Cela peut être répété pendant plusieurs générations et, avec chaque génération de retour croisé, la contribution de la race donneuse est réduite de moitié. Cependant, avec chaque retour croisé, les avantages de l’outcrossing sont également réduits de moitié. Il est donc important de trouver le bon équilibre entre l’outcrossing, le retour croisé et l’accouplement au sein de la race elle-même.
Divers aspects peuvent influencer le succès d’un schéma d’outcrossing, notamment le nombre de générations de retours croisés, le nombre de portées produites par outcross, si toutes les portées issues de l’outcross sont produites en une seule génération et/ou si les outcross se répètent dans le temps, et le nombre de chiots sélectionnés parmi les portées issues de l’outcross. Il n’est pas possible de déterminer expérimentalement la variation des résultats d’un outcross chez les chiens de pedigree, car la répétition est difficile à réaliser. Par conséquent, nous devons nous fier aux résultats théoriques. Dans cette étude, nous avons utilisé des simulations informatiques pour déterminer les effets de différents schémas d’outcrossing. Nous étions particulièrement intéressés par l’effet moyen des différents schémas sur le niveau moyen de consanguinité et le taux de consanguinité, ainsi que par la possible variation autour de cette moyenne. Plus en détail, nous avons examiné l’effet de :
Le nombre de retours croisés après l’outcross initial
Des outcross répétés
La taille de l’outcross : nombre de portées et chiots sélectionnés pour la reproduction
Nous avons également étudié dans quelle mesure les allèles présents dans la race donneuse mais absents dans la race réceptrice sont introduits dans cette dernière lors d’un outcross. Ensuite, nous avons examiné la situation inverse : dans quelle mesure les allèles présents dans la race réceptrice mais absents dans la race donneuse sont éliminés de la race réceptrice par un outcross. Ces dernières simulations ont été effectuées avec différents schémas d’outcross pour des allèles dont l’effet varie de complètement létal à bénéfique.
2 MATÉRIELS ET MÉTHODES
Les effets de l’outcrossing sur la consanguinité et la variation allélique ont été évalués avec un programme de simulation précédemment développé pour l’analyse de la gestion génétique chez les chiens de pedigree (Windig & Oldenbroek, 2015). La race Saarloos Wolfhond a été utilisée comme modèle pour la race à croiser. C’est une race néerlandaise issue d’un croisement entre un loup et un berger allemand effectué vers 1935. La race a été reconnue en 1975 par le Kennel Club néerlandais. Numériquement, la race est restée petite avec au maximum environ 25 portées nées par an. Les taux de consanguinité étaient élevés, atteignant jusqu’à 10 % par génération entre 1996 et 2001 (AVLS, 2012). Depuis, plusieurs troubles génétiques sont apparus et la taille
des portées a diminué. En 2016, une des organisations d’élevage a lancé un projet d’outcross pour contrer les effets négatifs de la consanguinité.
2.1 Simulations
Les paramètres reproductifs extraits des données de pedigree de la race de 2000 à 2010 ont été utilisés pour déterminer les entrées des simulations. Durant cette période, la population comptait en moyenne 28 femelles reproductrices et 11 mâles reproducteurs, produisant 14 portées par an pour un total de 68 chiots. L’âge moyen des parents à la naissance de leurs chiots était de 4,1 ans (= intervalle de génération), avec un maximum de 9 ans pour les pères et mères et un minimum de 2 ans pour les mères et 1 an pour les pères. La taille des portées était en moyenne de 4,9 chiots avec un maximum de neuf chiots. Ces valeurs ont été utilisées comme entrées pour le programme de simulation. La race a été simulée sur 100 ans, et chaque simulation a été répétée 50 fois pour déterminer la variation entre les répétitions. Cinquante simulations ont été choisies après un test de 1000 simulations et détermination de la variation des taux de consanguinité entre groupes de 50 simulations, qui était au maximum de 0,14 %. Dans toutes ces simulations, la race a été simulée sans outcross pendant les 80 premières années, tandis que les outcross pouvaient être simulés pendant les 20 dernières années.
Le programme de simulation comprend quatre étapes [détails dans (Windig & Oldenbroek, 2015)]. Dans la première étape, la population est mise en place selon les données fournies par l’utilisateur. La taille et la structure d’âge de la population sont maintenues constantes, comme c’est généralement le cas dans les populations captives lorsque la politique d’élevage ou la demande de jeunes animaux ne change pas. Dans la deuxième étape, les animaux sont accouplés. Chaque année, le même nombre de portées est né (déterminé par l’utilisateur). Pour produire une portée, une femelle est choisie au hasard parmi les femelles reproductrices disponibles et accouplée au hasard avec un mâle reproducteur. Les femelles ne peuvent avoir qu’une portée par an, tandis que les mâles peuvent avoir plusieurs portées. La distribution de la taille des portées est déterminée par les données saisies par l’utilisateur et reste la même tout au long de la simulation. Dans la troisième étape, le niveau de consanguinité des chiots nouveau-nés est calculé, ainsi que leur parenté avec tous les autres animaux vivants dans la population. Dans la dernière étape, les vieux animaux sont abattus et remplacés par de jeunes animaux. Tous les animaux restants prennent un an de plus. L’abattage des animaux est déterminé par la structure d’âge, et les animaux abattus dans une classe d’âge sont choisis au hasard. En spécifiant plus de classes d’âge, le chevauchement des générations est augmenté. Les animaux abattus sont remplacés par l’un des chiots nés cette année-là, choisi au hasard. Le niveau moyen de consanguinité par an et l’âge moyen des parents sont produits en sortie, à partir desquels les taux de consanguinité par génération peuvent être calculés.
Le programme de simulation a été étendu pour simuler plusieurs (sous-)populations simultanément, avec des échanges entre les sous-populations déterminés par l’utilisateur. Pour simuler l’outcross, deux populations ont été simulées : le Saarloos Wolfhond comme population réceptrice et une population donneuse. La population donneuse avait la même structure d’âge et distribution de taille des portées que la population réceptrice mais se composait de 50 mâles et 50 femelles reproducteurs, et sa taille effective était donc considérablement plus grande. Les deux populations ont d’abord été simulées séparément pendant 80 ans pour que les parentés et les niveaux de consanguinité se développent différemment dans les deux populations. La simulation de l’outcross a commencé à la 80e année.
Les résultats de la simulation, en particulier le taux de consanguinité et la contribution génétique des ancêtres donneurs à la population réceptrice, sont évalués pour les années 75 à 100, soit environ la période considérée par les associations de race pour un projet d’outcross. Le taux de consanguinité (ΔF) est calculé sur ces 25 ans en suivant Falconer et Mackay (1996) en utilisant la formule
[ \Delta F = \frac{F_{100} – F_{75}}{L} ]
où L est l’intervalle de génération et F75 et F100 les niveaux moyens de consanguinité dans la population respectivement aux années 75 et 100. La contribution génétique des ancêtres donneurs à un animal est calculée comme la moyenne de la contribution des deux parents. Un chiot issu d’un croisement entre un père 100% (= pur) donneur et une mère 100% réceptrice a donc une contribution de 50% de la population donneuse.
2.2 Schémas d’outcross
Plusieurs schémas d’outcross ont été simulés, différant par le nombre d’outcross et la combinaison avec des retours croisés.
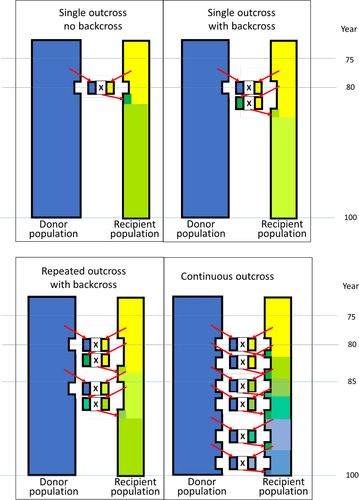
2.3 Croisement unique, sans rétro-croisement
Le schéma le plus simple était un croisement unique dans lequel une seule portée était engendrée par un père de la population donneuse. Les chiots issus du croisement étaient traités comme tous les autres chiots. Cela impliquait que, l’année suivant le croisement, les animaux éliminés étaient remplacés par des chiots issus d’accouplements avec ou sans croisement (les deux avec la même probabilité). Ensuite, le nombre de portées engendrées par des pères de la population donneuse a été augmenté, jusqu’à ce que les 14 portées de cette année soient engendrées par la population donneuse.
2.4 Croisement unique, avec rétro-croisement
Le deuxième schéma simulé était un croisement suivi d’une ou plusieurs générations de rétro-croisements. Dans la première année de l’événement de croisement, soit deux, soit quatre portées étaient engendrées par un père de la population donneuse. De chacune des portées produites, deux chiots étaient sélectionnés pour la reproduction l’année suivante et accouplés avec un père ou une mère de la population réceptrice. Si un seul chiot était né (9 % des portées), ce chiot était simplement sélectionné. Comme le nombre de portées nées de femelles de la race réceptrice restait constant, moins de portées étaient nées avec les deux parents de la race réceptrice les années où des femelles étaient utilisées dans le schéma de croisement. Le croisement initial était suivi de 1, 2, 3 ou 4 années de rétro-croisements. Les chiots produits par le dernier rétro-croisement étaient traités comme tous les autres chiots.
2.5 Croisement répété
Dans ces schémas, l’effet de répéter un croisement a été simulé. Cela a été fait pour un croisement impliquant deux portées, soit non suivi d’un rétro-croisement, soit suivi de deux rétro-croisements. Un croisement a été répété une ou deux fois. Le premier croisement a commencé à l’année 80, la première répétition à l’année 85 et la deuxième répétition à l’année 90.
2.6 Croisement continu
Le croisement continu était le dernier schéma simulé. Dans ce cas, chaque année, toutes les portées de la population réceptrice avaient une probabilité de 1 % d’être engendrées par un père de la population donneuse. Par conséquent, sur une période de 20 ans avec 14 portées par an, en moyenne 2,8 portées étaient engendrées par un père de la population donneuse, ce qui correspond à peu près au même nombre que celui produit dans un croisement unique d’une seule portée répété trois fois. La principale différence est qu’avec le schéma de croisement continu, plus ou moins de trois croisements peuvent se produire et que ces croisements sont répartis aléatoirement sur les années. Le croisement continu a été simulé pour imiter la situation où des croisements sont occasionnellement autorisés, ou effectués secrètement, avec des chiens sans pedigree officiel (appelés « look-alikes »). Le croisement continu a également été simulé avec une probabilité de 5 % et de 10 % d’être engendré par un père de la population donneuse.
2.7 Destin des allèles
En plus de l’effet du croisement sur la consanguinité, nous avons évalué le destin des allèles. À cet effet, le logiciel de simulation a été étendu avec des loci bialléliques sans liaison entre les loci. Au début de la simulation, chaque animal a reçu deux allèles par locus, où la probabilité qu’une variante spécifique se produise était basée sur sa fréquence allélique initiale (fournie par l’utilisateur). Dans les années suivantes, chaque chiot nouveau-né recevait au hasard un allèle de chaque parent. Dans les 80 premières années de la simulation sans croisement, les fréquences alléliques ont changé en raison de la sélection naturelle et de la dérive génétique, de sorte que les fréquences ont atteint des niveaux réalistes en fonction de leur influence sur la fitness.
Cinq types différents d’allèles ont été simulés dans cette recherche : (i) des allèles neutres, (ii) des allèles délétères qui réduisaient la survie des chiots nouveau-nés de 20 % lorsqu’ils étaient homozygotes, (iii) des allèles bénéfiques qui étaient le complément des allèles délétères et augmentaient ainsi la survie des chiots de 25 % lorsqu’ils étaient hétérozygotes ou homozygotes par rapport aux allèles homozygotes non bénéfiques, (iv) des allèles létaux pour lesquels les animaux mouraient à l’âge de 3 ans lorsqu’ils étaient homozygotes, et (v) des allèles complètement létaux pour lesquels tous les animaux homozygotes mouraient à la naissance. L’accouplement et l’héritage des allèles étaient aléatoires, mais une sélection contre les allèles s’est produite parce que les chiots homozygotes pour les allèles létaux mouraient (soit à la naissance, soit après 3 ans, ou avec une probabilité de 20 % selon le type). Les simulations ont d’abord été effectuées avec l’allèle ne se trouvant que dans la population réceptrice et absent dans la population donneuse. Cela a été fait pour déterminer si un croisement pouvait éliminer ou diminuer la fréquence de l’allèle. Ensuite, des simulations ont été effectuées avec l’allèle ne se trouvant que dans la population donneuse et absent dans la population réceptrice. Cela a été fait pour déterminer à quelle fréquence l’allèle était introduit par croisement dans la population réceptrice et, si c’était le cas, quelle fréquence il pouvait atteindre dans les 20 prochaines années. Pour atteindre des fréquences réalistes des différents allèles, les simulations ont d’abord été exécutées pendant 80 ans sans croisement, de sorte que la sélection et la dérive génétique modifient les fréquences initiales. Tous les allèles ont commencé à une fréquence de 50 %, et on s’attendait à ce que la sélection diminue la fréquence des allèles délétères et létaux et augmente la fréquence des allèles bénéfiques. Les changements dus à la dérive génétique étaient aléatoires en direction et plus importants dans la population réceptrice que dans la population donneuse, en raison de la taille effective de population plus grande de cette dernière. Pour chaque type d’allèle, cinq loci ont été simulés et les simulations ont été répétées 25 fois, de sorte qu’au total, 125 allèles par type ont été simulés. Ainsi, dans une simulation donnée, cinq loci non liés du même type ont été simulés.
Les changements de fréquence allélique ont été évalués pour deux des schémas de croisement simulés. Le premier était le croisement impliquant deux portées, suivi de deux rétro-croisements et répété deux fois, car c’est le type de croisement que la société de race envisage. Le deuxième type était le croisement continu où chaque portée avait une probabilité de 10 % d’être engendrée par un père de la population donneuse, car c’était le type le plus efficace analysé.
3 RÉSULTATS
3.1 Sans croisement
Le taux de consanguinité dans la race réceptrice (le Saarloos Wolfhond simulé) sans croisement était de 2,1 % par génération, entraînant un niveau de consanguinité moyen de 0,36 à l’année 75 et de 0,45 à l’année 100 (Figure 2). Comme prévu, le taux de consanguinité dans la population donneuse était considérablement plus faible, à 0,8 %. Les taux de consanguinité variaient considérablement entre les simulations, pour la population réceptrice entre 1,5 % et 3,2 %, et pour la population donneuse entre 0,7 % et 1,0 %. La simulation a donc confirmé que les taux de consanguinité pour la population réceptrice seront élevés si aucune mesure n’est prise.
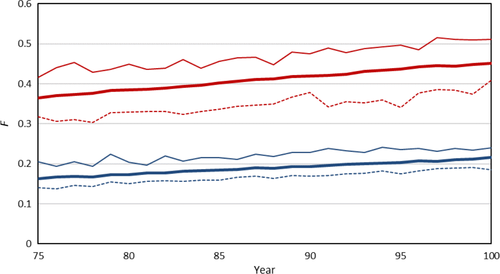
3.2 Croisement unique, sans rétro-croisement
Un croisement unique, avec un seul mâle produisant une seule portée et sans rétro-croisement, a réduit le taux de consanguinité à une moyenne de 1,7 % (Tableau 1). Cependant, il y avait une variation considérable entre les simulations, avec un taux de consanguinité minimum de 0,3 % et un maximum de 3,2 %. Le croisement avec plus de mâles a encore réduit les taux de consanguinité moyens, jusqu’à 0,1 % lorsque les 14 portées de la race cette année-là étaient le résultat d’un croisement. La variation des taux de consanguinité était considérable. Dans quelques cas, pour huit et 14 portées croisées, le niveau de consanguinité a même diminué. D’autre part, des taux de consanguinité bien supérieurs à 2 % se sont également produits, pour jusqu’à huit portées produites par croisement. La contribution génétique de la population donneuse à la population réceptrice a augmenté avec le nombre de portées croisées, jusqu’à une moyenne de 13,2 % lorsque les 14 portées étaient croisées. La variation de la contribution donneuse était toujours importante, avec pour tous les nombres de portées, sauf pour les 14 portées croisées, des simulations où la contribution donneuse était complètement éliminée.
Tableau 1. Taux de consanguinité (ΔF en % ; entre l’année 75 et l’année 100) et contribution génétique de la population donneuse à l’année 100 pour un croisement unique, non suivi de rétro-croisements. Le croisement a eu lieu à l’année 80 où un ou plusieurs mâles de la population donneuse ont été utilisés pour produire une ou plusieurs portées.
| Number of litters | ΔF and Ne year 75 to 100 (%) | Donor contribution in year 100 (%) | |||
|---|---|---|---|---|---|
| Mean | (95% c.i.) | N e | Mean | (Min.–Max.) | |
| 0 | 2.1 | (1.0–3.0) | 25 | 0.0 | (0–0) |
| 1 | 1.7 | (0.7–2.8) | 29 | 1.5 | (0–6.7) |
| 2 | 1.7 | (0.5–2.8) | 29 | 2.7 | (0–15.3) |
| 4 | 1.4 | (0.2–2.6) | 37 | 4.3 | (0–15.6) |
| 8 | 0.9 | (−0.7 to 2.5) | 54 | 7.7 | (0–23.3) |
| 14 | 0.1 | (−1.5 to 1.8) | 398 | 13.2 | (0.9–29.4) |
3.3 Croisement unique, avec rétro-croisements
Un croisement unique suivi d’une ou plusieurs générations de rétro-croisements a diminué l’effet du croisement, ou même entraîné des taux de consanguinité plus élevés comparés à l’absence de croisement (Tableau 2). Dans le cas où deux portées étaient croisées, il y avait peu d’effet du croisement lorsqu’il était suivi d’une génération de rétro-croisement (le taux de consanguinité moyen a diminué de 2,1 % à 2,0 %), aucun effet avec deux ou trois rétro-croisements, et une légère augmentation (jusqu’à 2,2 %) avec quatre rétro-croisements. Pour tous ces schémas, la variation des taux de consanguinité entre les simulations était importante, avec des taux allant d’environ 1 % à 3 %. Dans le cas où quatre portées étaient croisées, le taux de consanguinité diminuait encore lorsque un ou deux rétro-croisements étaient utilisés, mais augmentait avec trois ou quatre rétro-croisements. La variation entre les simulations était toujours grande, surtout dans le schéma avec quatre rétro-croisements, où le taux de consanguinité maximum était de 3,2 %. À chaque rétro-croisement, la contribution moyenne de la population donneuse à la population réceptrice diminuait, jusqu’à 0,5 % ou moins lorsque trois rétro-croisements ou plus étaient utilisés. L’élimination complète de la contribution donneuse s’est produite dans tous les schémas de rétro-croisement, tandis que le maximum observé, pour un croisement impliquant quatre portées suivi d’un rétro-croisement, était juste au-dessus de 9 %.
Tableau 2. Taux de consanguinité (ΔF) et niveau (F) pour un croisement unique suivi d’une ou plusieurs générations de rétro-croisements. Le croisement a eu lieu à l’année 80 où deux ou quatre mâles d’une population donneuse ont été utilisés pour produire quatre portées. De chaque portée, deux chiots ont été sélectionnés et rétro-croisés l’année suivante avec la population réceptrice.
| Number of males | Number of backcross generations | ΔF year 75 to 100 (%) | N e | Donor contribution in year 100 | ||
|---|---|---|---|---|---|---|
| Mean | (95% c.i.) | Mean | (Min.–Max.) | |||
| 0 no outcross | 0 | 2.1 | (1.0–3.0) | 24 | 0.0 | (0–0) |
| 2 | 0 | 1.7 | (0.5–2.8) | 29 | 2.7 | (0–15.3) |
| 1 | 2.0 | (0.8–3.2) | 25 | 1.1 | (0–6.5) | |
| 2 | 2.1 | (1.1–3.1) | 25 | 0.7 | (0–3.2) | |
| 3 | 2.1 | (1.3–3.1) | 24 | 0.2 | (0–1.4) | |
| 4 | 2.2 | (1.2–3.1) | 22 | 0.1 | (0–0.5) | |
| 4 | 0 | 1.4 | (0.2–2.6) | 35 | 4.3 | (0–15.6) |
| 1 | 1.6 | (0.4–2.8) | 31 | 2.8 | (0–9.4) | |
| 2 | 2.0 | (0.9–3.1) | 25 | 1.4 | (0–4.0) | |
| 3 | 2.1 | (1.2–3.0) | 23 | 0.5 | (0–1.9) | |
| 4 | 2.2 | (1.2 – 3.1) | 22 | 0.4 | (0 –1.1) | |
3.4 Croisement répété
Les croisements répétés ont réduit davantage les taux de consanguinité (Tableau 3). Lorsque le croisement a été effectué trois fois avec deux portées croisées, le taux de consanguinité sans rétro-croisement a diminué à 1,0 % (Tableau 3, Figure 3). La réduction était moindre lorsque le croisement était suivi de deux rétro-croisements. Le niveau moyen de consanguinité était alors de 1,8 % pour trois répétitions. Dans tous les cas, la variation entre les simulations était considérable et des taux de consanguinité supérieurs à 2,5 % se sont produits. La contribution de la population donneuse à la population réceptrice à l’année 100 a augmenté, comparée à aucune répétition. Cependant, dans certaines simulations, l’élimination complète de la contribution de la population donneuse s’est produite pour chaque scénario évalué.
Tableau 3. Taux de consanguinité (ΔF) et niveau (F) pour des schémas sans ou avec un ou plusieurs croisements. Dans chaque schéma, deux mâles ont produit deux portées dont deux chiots par portée ont été sélectionnés pour être rétro-croisés ou ajoutés au pool d’animaux reproducteurs.
| Number of backcrosses following each outcross | Number of outcrosses | ΔF year 75 to 100 (%) | N e | Donor contribution in year 100 (%) | ||
|---|---|---|---|---|---|---|
| Mean | (95% c.i.) | Mean | (Min.–Max.) | |||
| 0 no outcross | 0 | 2.1 | (1.0–3.0) | 24 | 0 | (0–0) |
| 0 | 1 | 1.7 | (0.5–2.8) | 29 | 2.7 | (0–15.3) |
| 2 | 1.5 | (−0.1 to 3.0) | 34 | 3.8 | (0–12.3) | |
| 3 | 1.0 | (−0.6 to 2.7) | 48 | 6.1 | (0–18.0) | |
| 2 | 1 | 2.1 | (1.1–3.1) | 24 | 0.7 | (0–3.2) |
| 2 | 1.9 | (0.7–3.1) | 26 | 1.3 | (0–8.9) | |
| 3 | 1.8 | (0.9–2.8) | 28 | 1.8 | (0–4.9) | |
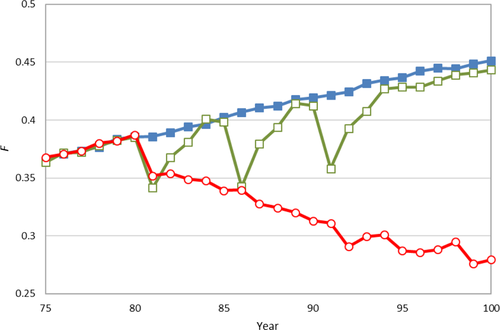
3.5 Croisement continu
Le croisement continu de certains animaux avec la population donneuse a réduit les taux de consanguinité et, dans la plupart des cas, également les niveaux de consanguinité (c’est-à-dire, taux de consanguinité < 0). Avec une chance de 1 % qu’une portée soit engendrée par un mâle de la population donneuse—donc en moyenne une portée croisée tous les 7 ans—la consanguinité était en moyenne comparable à une ou deux croisements uniques. Avec un échange de 5 % ou 10 %, les taux de consanguinité étaient négatifs en moyenne (Tableau 4). La variation des niveaux de consanguinité entre les simulations était considérable avec le croisement continu. Pour une chance de croisement de 10 %, le niveau de consanguinité a immédiatement chuté au niveau de la population donneuse dans certaines simulations, tandis que dans d’autres, le niveau de consanguinité à l’année 100 était encore supérieur à celui de la population donneuse (Figure 3). La contribution de la population donneuse était, avec un taux de croisement de 10 %, en moyenne de 25,2 % à l’année 100, avec un minimum de 12,5 % et un maximum de 45,5 %.
Tableau 4. Taux de consanguinité (ΔF) et niveau (F) pour un schéma de croisement continu. À chaque génération, une portée de la population réceptrice a une chance de 1 %, 5 % ou 10 % d’être engendrée par un mâle de la population donneuse.
| Percentage litters sired by donor breed | ΔF year 75 to 100 (%) | Donor contribution in year 100 (%) | ||
|---|---|---|---|---|
| Mean | (95% c.i.) | Mean | (Min.–Max.) | |
| 0 no outcross | 2.1 | (1.0–3.0) | 0 | (0–0) |
| 1% | 1.7 | (−0.3 to 3.4) | 2.7 | (0–13.2) |
| 5% | −0.2 | (−2.6 to 2.1) | 14.6 | (0–35.5) |
| 10% | −1.8 | (−3.6 to 0.0) | 25.2 | (12.5–45.3) |
3.6 Diversité allélique
3.6.1 Allèles initialement présents uniquement dans la population réceptrice
Dans les 75 premières années de la simulation, les fréquences alléliques dans la population réceptrice ont changé en raison de la dérive génétique et de la sélection naturelle. La fréquence des allèles neutres a peu changé en moyenne (0,506 à l’année 75, comparé à l’initiale de 0,5). Cependant, il y avait une variation considérable de la fréquence des allèles entre les différents loci, allant de 0 % (éliminé) à 100 % (fixé), avec toutes les fréquences intermédiaires se produisant à peu près au même taux (Figure 4). L’allèle complètement létal, en revanche, a disparu pour 70,8 % des allèles simulés et sa fréquence moyenne était de 0,034 à l’année 75. Lorsque l’allèle était létal après 3 ans, il a disparu pour 63,5 % des allèles simulés. L’allèle délétère a disparu pour 29,4 % des allèles simulés, et l’allèle bénéfique n’a jamais été perdu. L’allèle bénéfique a été cependant fixé dans 17,9 % des cas, tandis que les allèles de tous les autres types n’ont jamais été fixés avant le croisement.
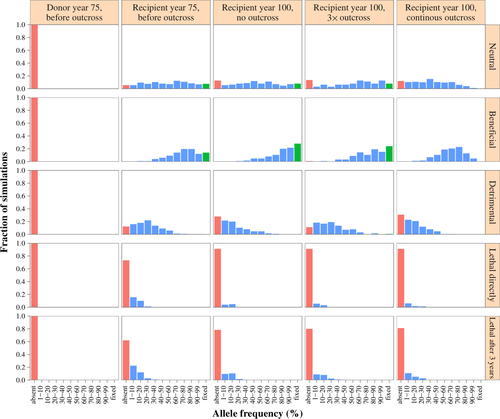
Lorsque aucun croisement n’a été effectué, la dérive génétique et la sélection naturelle ont continué à modifier les fréquences alléliques. Plus d’allèles ont été éliminés pour tous les types sauf les allèles bénéfiques, pour lesquels davantage d’allèles sont devenus fixés. Par exemple, le pourcentage d’allèles létaux éliminés est passé de 70,8 % après 75 ans à 91,2 % après 100 ans. Le pourcentage d’allèles bénéfiques qui ont été fixés a augmenté de 17,9 % à 28 % sans croisement. Les fréquences alléliques après un croisement répété (3 × croisement, chacun suivi de deux rétro-croisements) avec une population donneuse dans laquelle l’allèle était absent, étaient très similaires aux fréquences observées sans croisement. Par exemple, l’allèle bénéfique a disparu dans une seule des simulations après le croisement, tandis que la fixation par sélection a continué à se produire, et après le croisement, 24 % des allèles bénéfiques étaient fixés contre 28 % sans croisement. Le pourcentage d’allèles létaux éliminés était le même avec et sans croisement. Les changements de fréquences étaient plus importants lorsque la population réceptrice était continuellement croisée avec la population donneuse. Par exemple, aucun des allèles bénéfiques n’est resté fixé après le croisement continu, et 91,2 % des allèles létaux ont été éliminés (Figure 4).
3.6.2 Allèles initialement présents uniquement dans la population donneuse
Dans les simulations où l’allèle se trouvait initialement uniquement dans la population donneuse, la fréquence moyenne après 75 ans était très similaire à celle de la population réceptrice pour les simulations dans lesquelles l’allèle se trouvait initialement uniquement dans la population réceptrice (Figure 5, première ligne). La variance, cependant, était plus faible, en accord avec la plus petite taille effective de la population et une dérive génétique plus importante dans la population réceptrice.
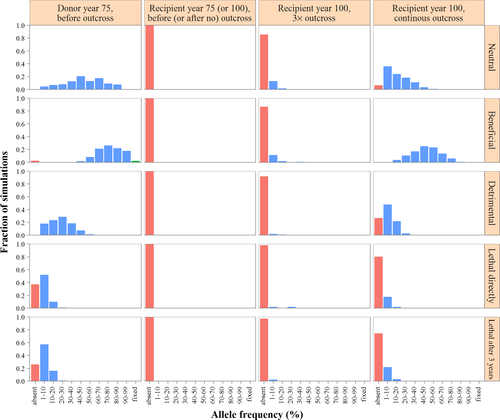
Après un croisement répété (3× croisements externes, chacun suivi de deux rétro-croisements) avec la population réceptrice où l’allèle était absent, l’allèle est resté absent dans la plupart des cas. Lorsqu’il y avait croisement externe, des allèles étaient introduits plus souvent dans la population réceptrice. Des allèles bénéfiques ont été introduits dans toutes les simulations. En revanche, l’allèle létal est resté absent dans 98,2% des simulations après 3× croisements externes suivis de deux rétro-croisements, et dans 80,4% après des croisements externes continus.
4 DISCUSSION
Dans cette étude, nous avons évalué l’effet de différents schémas de croisement externe sur le niveau et le taux de consanguinité, ainsi que sur le sort des allèles neutres, bénéfiques, létaux et délétères. En général, le croisement externe avait un effet limité sur les niveaux de consanguinité. Surtout lorsqu’un croisement externe était suivi d’un ou plusieurs rétro-croisements, l’effet était faible. Lorsque quatre rétro-croisements étaient utilisés, le niveau moyen de consanguinité augmentait même légèrement. Cela était dû au nombre réduit de portées disponibles pour l’élevage pur. Lorsqu’un croisement externe était suivi d’un rétro-croisement, il devait être répété (au moins deux fois en cas de deux portées croisées) pour avoir un effet notable. Les taux de consanguinité inférieurs à 1% ne se produisaient qu’avec des croisements externes continus.
L’effet du croisement externe est souvent limité malgré le fait que la F1 ait un niveau de consanguinité de 0%. Plusieurs raisons expliquent cet effet limité. La raison principale est que l’effet du croisement externe est réduit de moitié à chaque génération de rétro-croisement. Par exemple, si la F1 est croisée avec un chien de race pure, trois des quatre grands-parents sont de la population réceptrice, et le niveau de consanguinité attendu est la moitié de la parenté avant le croisement externe. La deuxième raison est que lorsque la taille effective de la population reste petite, le taux de consanguinité revient au niveau antérieur au croisement externe. Dans les cas où une grande proportion des animaux est croisée, le nombre de chiens de race pure diminue, et lorsque seulement quelques-uns restent pour les rétro-croisements, la taille effective de la population peut même diminuer, comme c’était le cas lorsqu’un croisement externe était suivi de quatre générations de rétro-croisements.
Le taux de consanguinité variait beaucoup après les croisements externes. Dans les simulations, l’accouplement et la survie après un croisement externe étaient aléatoires, et par conséquent, la reproduction des descendants du croisement externe variait selon les essais. Dans certains essais, les descendants étaient à peine utilisés, ce qui entraînait des taux de consanguinité plus élevés et une élimination complète des allèles donneurs. Dans d’autres essais, les descendants étaient fréquemment utilisés, les taux de consanguinité étaient plus faibles et les contributions des donneurs plus élevées. Il est donc important de gérer la population après un croisement externe afin d’augmenter la taille effective de la population. Plusieurs options de gestion génétique existent, mais l’une des plus efficaces est la méthode de parenté moyenne, c’est-à-dire exclure de la reproduction les animaux ayant une parenté supérieure à la moyenne avec tous les autres candidats à la reproduction (Lewis & Windig, 2017). Cette méthode peut être particulièrement efficace après un croisement externe, car les descendants d’un croisement externe auront initialement une parenté moyenne faible, mais une fois que la contribution génétique d’un chien utilisé dans un croisement externe atteint une valeur trop élevée, ses descendants peuvent être exclus de la reproduction. Nous avons testé la méthode de parenté moyenne pour le scénario de deux croisements externes suivis chacun de trois rétro-croisements, pour lesquels nous avons simulé la méthode de parenté moyenne après le dernier rétro-croisement, donc de l’année 92 à 100. Le taux de consanguinité de 1,8% sans parenté moyenne (Tableau 3, dernière ligne) est passé en moyenne à 1% (avec un IC à 95% de 0,2% à 1,8%), tandis que la contribution de la population donneuse a augmenté en moyenne à 4,4%, allant de 0,5% à 4,0%. Ainsi, une bonne gestion génétique après un croisement externe est nécessaire pour profiter de la diversité génétique introduite.
Les taux de consanguinité et les tailles de populations effectives varient selon les races (Wijnrocx, Francois, Stinckens, Janssens & Buys, 2016). Le Saarloos Wolfhond simulé dans cette étude est à l’extrémité inférieure des tailles de population effective et a été choisi car des croisements externes sont typiquement initiés pour ces races. Pour les races ayant une taille de population effective plus élevée, un croisement externe aura encore moins d’effet. Une race non apparentée a été simulée comme race donneuse. En pratique, des races apparentées seront utilisées. Par conséquent, l’effet d’un croisement externe peut être encore plus faible que celui simulé dans cette étude. Cependant, pour les chiens de race, même les chiens de races apparentées n’ont jamais été autorisés comme parents, donc des ancêtres communs se trouvent il y a de nombreuses générations. Par exemple, le Saarloos Wolfhond simulé dans cette étude a vu le jour il y a plus de 80 ans, soit en moyenne 20 générations. Ainsi, l’effet réduit du croisement avec une race apparentée au lieu d’une race non apparentée sur les niveaux et taux de consanguinité après un croisement externe sera donc marginal.
Lorsque le croisement externe est utilisé dans le but d’éliminer (ou d’introduire) un ou plusieurs allèles dans la population, la génomique peut aider à déterminer quels animaux utiliser pour les rétro-croisements. Des procédures ont été développées pour une telle introgression assistée par génomique (Hospital, Chevalet, & Mulsant, 1992; Wall, Visscher, Hospital, & Woolliams, 2005) et peuvent accélérer le processus. Utiliser la génomique pour soutenir les croisements externes avec l’objectif général d’augmenter la diversité génétique et prévenir davantage de dépression consanguine sera plus difficile. Idéalement, les allèles indésirables devraient être remplacés sans en introduire d’autres également indésirables. Cependant, l’identification des gènes d’intérêt est un défi majeur. Après avoir identifié un objectif d’élevage tel qu’un indice combinant le standard de la race avec la longévité et la fertilité, combiner le croisement externe avec la sélection génomique peut être la meilleure voie à suivre, comme l’introgression combinée avec la sélection génomique a prouvé son succès dans un programme de sélection combinant la sélection pour le mérite génétique avec l’introgression d’un allèle unique (Gaspa, Veerkamp, Calus, & Windig, 2015).
L’introgression non désirée d’allèles délétères (inconnus) provenant d’une race donneuse est souvent utilisée comme argument contre les croisements externes. Puisque probablement tous les animaux portent des allèles récessifs délétères, cela peut effectivement être le cas. Cependant, l’introgression d’allèles bénéfiques est également possible. La probabilité que différents allèles soient présents dans la race donneuse dépend de la proximité de la relation entre les races. Plus les races sont apparentées, plus la probabilité que les mêmes allèles soient présents est grande, qu’ils soient désirables ou non. Par conséquent, l’introduction par croisement externe d’allèles non présents dans la race peut être encore plus faible que celle simulée dans cette étude, et les fréquences des allèles introduits dérivées ici peuvent être considérées comme une limite supérieure.
Un autre aspect important à prendre en compte est que la sélection naturelle passée aura influencé les fréquences actuelles de sorte que les allèles délétères se trouvent généralement à des fréquences plus faibles que les allèles bénéfiques. Dans cette étude, nous montrons qu’en raison de cela, il est en fait plus probable d’introduire des allèles bénéfiques que délétères pour les allèles présents dans la race donneuse et absents dans la race réceptrice. Les allèles létaux ne peuvent rester à des fréquences faibles que dans une population avec une taille effective élevée, en raison de la sélection contre eux à des fréquences plus élevées.
5 CONCLUSION
Sauf si les croisements externes sont répétés régulièrement ou en continu, leur effet sur la consanguinité et les fréquences alléliques est limité. Bien que les chiots soient initialement nés avec des coefficients de consanguinité de 0, les niveaux et taux de consanguinité peuvent rapidement revenir aux niveaux précédents. Il reste donc important d’augmenter la taille effective de la population réceptrice avec d’autres méthodes. Un croisement externe peut aider à ramener les niveaux de consanguinité à des niveaux inférieurs comme point de départ pour réduire définitivement les taux de consanguinité, par exemple en modifiant la structure de la population. À cet égard